In my previous blog post I shared some experiments with wavelets using available online tools. In order to build better understanding on how to apply Morlet wavelets in detecting Morse code in noisy signals I wrote a little test application using Octave. The application creates noisy Morse code and does Continuous Wavelet Transform (CWT) using modified Morlet wavelet as well as Short Term Fourier Transform (STFT). The Octave application allows changing various parameters and visualizing the impact on the plotted graphs and images. See discussion on modification to Morlet wavelet below.
The starting point was original noisy Morse code signal that has -12.2 dB SNR as shown in the figure 1 below. It is virtually impossible to detect the Morse signal buried in the noise. When listening the audio I can hear a faint sound in the noise but I have much difficulties recognizing any of the characters.
For reference, the signal-to-noise ratio calculation is done the following way:
SNR=20*log10(norm(morsecode)/norm(morsecode-noisey_morsecode));
 |
| Figure 1. Morse code with -12.2 dB SNR (signal-to-noise ratio) |
To discover the Morse code signal I used Short Time Fourier Transformation (STFT) with the following parameters ( x contains noisy audio, sampling rate is Fs=4000 )
z = stft(x,1/Fs,4,128,1,512);
A very faint Morse signal is now visible at 600 Hz frequency as a horizontal pattern of "dits and "dahs" in figure 2. below. It is very difficult to "read" from this figure 3 below what the message is. Some "dits" and "dahs" are more visible but noise makes it difficult to detect the pattern or to decode the message.
 |
| Figure 2. Waterfall spectrogram of the Morse code with -12.2dB SNR. |
Modified Morlet Wavelet power spectrum is shown on figure 3. On Scale axis (vertical) you can see at S = 8 as a horizontal pattern of lighter "dits" and "dahs". Looking at the pattern you can almost see "dah-dit-dah-dit" "dah dah dit dah" "dah dit dit" "dit" "dit dah" "dah dah dit" "dit dah dah dah dah" "dit dah dit dit" "dit" aka "CQ DE AG1LE". This represents the peak energy of the power spectrum after Wavelet transformation. I am taking absolute value to show the envelope of the wavelet better (see morlet.m file below, calculation is done by this line: coeffs(k,:)=abs(fftshift(ifft(fft(w).*fft(sigin)))); )
 |
| Figure 3. Wavelet Power Spectrum of the Morse code with -12.2 dB SNR |
I plotted Wavelet coefficient C(t,8) values (corresponding Scale = 8 above) on x-y graph below in figure 4. Morse code "dits" and "dahs" are quite visible as signal peaks above threshold value of 2000. Note that these are abs(C(t,8)) values and low pass filtered to show envelope better. See morletdemo.m below for details.
 |
| Figure 4. Modified Morlet coefficient C(8) values. |
Original Morlet wavelets (scales 1 to 16 shown below in figure 5.) have variable wavelet pulse length and frequency as follows:
for k=1:scale,
t=(-M/2:M/2-1);
% Calculate Morelet Wavelet w=e-(at^2)*cos(2*pi*fo*t)
const = 1/(sigma*K*sqrt(k)); % k impacts relative amplitude
e = exp(-((sigma*t/k).^2)); % k impacts pulse length (t/k)
phase = cos(2*pi*fo*t/k); % k impacts frequency
w = const*e.*phase;
plot(w)
end
While experimenting with these wavelets it was quite difficult find the optimal wavelet to extract signal from noise.
 |
| Figure 5. Morlet wavelets 1...16 |
Looking at the impact of various parameters it became obvious that by modifying the wavelet to keep the duration constant improves the situation a lot. I modified a single line and the corresponding wavelet graph is below in figure 6.
e = exp(-((sigma*t).^2)); % removed k to keep the wavelet duration constant.
Note that wavelet bandwidth sigma depends on Morse speed - I did several experiments and established the following relationship sigma = (1.2/speed)/w where w is the number of the wavelet.
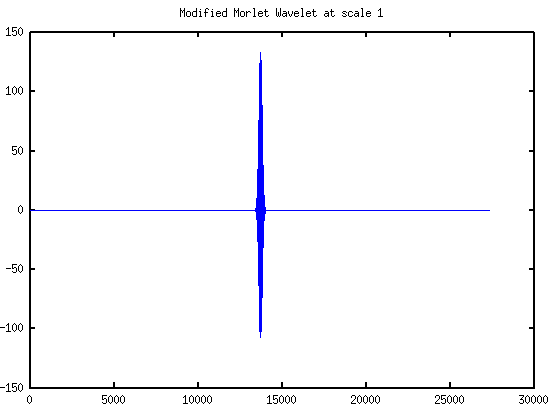 |
| Figure 6. Morlet Wavelet |
CONCLUSIONS
With a small modification to Morlet wavelet the CWT works better than STFT in extracting the signal from the noise even at -12 dB SNR. There are many similarities to Matched Filter method that I described in this blog post. Perhaps the main difference is the selected wavelet shape (Morlet) and the fact we use FFT to make the convolution very fast.
Further work could include the following tasks:
- program the modified Morlet Wavelet algorithm in C++
- implement this functionality in FLDIGI CW decoder module
- test Wavelet based decoder with real life signals from HF bands
SOFTWARE
The Octave scripts are listed below. The above results were created by running the following command on Octave:
% noise level, signal freq, sampling rate, morsespeed
morletdemo(2,600,4000,20)
The software prints these lines
text = CQ de AG1LE
file = CQ.wav
SNR =-12.226566
Fo = 1.2000
sigma = 0.0075000
and plots the figures.
File Morlet.m
% Project 2
% Time-Frequency Representations
% Andy Doran, modified by AG1LE Mauri Niininen
%
% function coeffs = cwvt(sigin,scale,quiet,sigma,fo)
%
% sigin = sampled input signal (Should be a row vector)
% scale = number of real, positive scale you want (1:scales)
% quiet = plot suppression
% 1 -> suppress all plots
% 2 -> suppress wavelet plots only
% 3 -> suppress scalogram only
% sigma =0.015625; Morlet Wavelet bandwidth
% fo = 0.25; Center frequency of Wavelet
% coeffs = scales-by-length(sigin) matrix returning CWT of sigin at
% each scale from 1 to scale
%
% This function takes an input signal and computes the Continuous Wavelet
% Transform at different scales using a sampled Morlet Wavelet
%
% Morelet Wavelet w(t) = (1/sigma*K)*exp-((sigma*t)^2)*cos(2*pi*fo*t)
function coeffs = morlet(sigin,scale,quiet,sigma,fo)
K = 1; % Not sure what this is, so set to 1
M = length(sigin);
coeffs = zeros(scale,M);
for k=1:scale,
t=(-M/2:M/2-1);
% Calculate Morelet Wavelet w=e-(at^2)*cos(2*pi*fo*t)
const = 1/(sigma*K*sqrt(k)); % k impacts relative amplitude
e = exp(-((sigma*t).^2)); % removed k to keep the wavelet duration constant
phase = cos(2*pi*fo*t/k); % k impacts frequency
w = const*e.*phase;
% Plot wavelet in time domain and frequency domain
if ((quiet ~= 1) & (quiet ~= 2))
figure(3)
if (k == 1) % Clear plot on initial run-through
clf
end
subplot(scale,2,(2*k)-1)
plot(w)
txt = ['Modified Morlet Wavelet at scale ', num2str(k)];
title(txt)
%figure(4)
%if (k == 1) % Clear plot on initial run-through
% clf
%end
subplot(scale,2,2*k)
plot(abs(fft(w)))
txt = ['Frequency Spectra of Morlet Wavelet at scale ', num2str(k)];
title(txt)
end
% Calculate CWT of sigin using circular convolution
% coeffs(k,:)=ifft(fft(w).*fft(sigin));
coeffs(k,:)=abs(fftshift(ifft(fft(w).*fft(sigin))));
end
% Coeffs should be real anyway, this just accounts for numerical error
% in circular convolution that may give small imaginary parts
coeffs = real(coeffs);
% Plot scalogram and check against MATLAB's CWT routine
if ((quiet ~= 1) & (quiet ~= 3))
figure(1)
%clf
map = jet();
colormap(map);
imagesc(coeffs);
axis xy;
txt = ['abs|C(t,s)| for s = 1 to ' num2str(scale)];
title(txt)
ylabel('s')
xlabel('t')
figure(2);
plot(sigin);
title('original signal');
%figure(4);
%clf
%cwt(sigin,1:scale,'morl','plot'); % Call MATLAB's CWT routine
%title('CWT Output from MATLAB')
end
File stft.m
function y = STFT(x, sampling_rate, window, window_length, step_dist, padding)
%
% y = STFT(x, sampling_rate, window, window_length, step_dist, padding)
%
% STFT produces a TF image of "x".
% The output is also stored in "y".
%
% For "window", use one of the following inputs:
% rectangular = 1
% Hamming = 2
% Hanning = 3
% Blackman-Tukey = 4
%
% The time scale is associated with the center of the window,
% if the window is of odd length. Otherwise, the window_length/2
% is used. "Step_dist" determines the stepping distance between the number
% of samples, and is arranged to maintain the proper time index
% provided by "sampling_rate" in seconds. "Padding" is the
% total length of the windowed signal before the fft, which is
% accomplished by zero padding.
%
% Developed by Timothy D. Dorney
% Rice University
% April, 1999
% tdorney@ieee.org
%
% Coded using MATLAB 5.X.X.
% See http://www.clear.rice.edu/elec631/Projects99/mit/index2.htm
%
% REVISION HISTORY
%
% VERSION 1.0.0 APR. 21, 1999 TIM DORNEY
%
if (nargin ~= 6)
disp('STFT requires 6 input arguments!')
return;
end
if ((window < 1) | (window > 4))
window = 1;
disp('The argument "window" must be between 1-4, inclusively. Window set to 1!');
end
if ((step_dist < 1) | (round(step_dist) ~= step_dist))
step_dist = 1;
disp('The argument "step_dist" must be an integer greater than 0. Step_dist set to 1!');
end
if (sampling_rate <= 0)
disp('The argument "sampling_rate" must be greater than 0.');
break;
end
if (padding < window_length)
padding = window_length;
disp('The argument "padding" must be non-negative. Padding set to "window_length"!');
end
if (window == 1)
WIN = ones(1,window_length);
elseif (window == 2)
WIN = hamming(window_length)';
elseif (window == 3)
WIN = hanning(window_length)';
elseif (window == 4)
WIN = blackman(window_length)';
end
[m,n] = size(x);
if (m ~= 1)
X = x';
else
X = x;
end
[m,n] = size(X);
if (m ~= 1)
disp('X must be a vector, not a matrix!');
break;
end
LENX = length(X);
IMGX = ceil(LENX/step_dist);
if (padding/2 == round(padding/2))
IMGY = (padding/2) + 1;
else
IMGY = ceil(padding/2);
end
y = zeros(IMGX,IMGY);
if (window_length/2 == round(window_length/2))
CENTER = window_length/2;
x_pad_st = window_length - CENTER - 1;
x_pad_fi = window_length - CENTER;
else
CENTER = (window_length+1)/2;
x_pad_st = window_length - CENTER;
x_pad_fi = window_length - CENTER;
end
X = [zeros(1,x_pad_st) X zeros(1,x_pad_fi)];
iter = 0;
for kk = 1:step_dist:LENX
iter = iter + 1;
XX = X(kk:(kk + window_length - 1));
YY = XX .* WIN;
ZZ = abs(fft(YY, padding));
y(iter,:) = ZZ(1:IMGY);
end
figure(6);
freq = (1/sampling_rate)/2;
imagesc([0:(step_dist*sampling_rate):(sampling_rate*(LENX-1))], ...
[0:(freq/(IMGY-1)):freq],y');
xlabel('Time (seconds)');
ylabel('Frequency (Hz)');
axis('xy')
File morletdemo.m
function morletdemo(noisy,freq,Fs,speed);
x = morse('CQ de AG1LE','CQ.wav',noisy,freq,Fs,speed);
w = 8; % peak will be at wavelet # w
Fo = freq / (Fs/w) % tell wavelet transform where wavelet center frequency is
sigma = (1.2/speed)/w % wavelet bandwidth - impacts time resolution
c = morlet(x',16,2,sigma,Fo); % do Morlet wavelet transform
y = filter(ones(1,20)/20,1,c(w,:)); % y = low pass filter C(t,w) wavelet
figure(4)
plot(y); % plot C(t,w) envelope
z = stft(x,1/Fs,4,128,1,512); % plot spectrogram of the signal using Short Term FFT
end;
File morse.m
function code=morse(varargin)
% MORSE converts text to playable morse code in wav format
%
% SYNTAX
% morse(text)
% morse(text,file_name);
% morse(text,file_name,noise_multiplier);
% morse(text, file_name,noise_multiplier,code_frequency);
% morse(text, file_name,noise_multiplier,code_frequency,sample_rate);
% morse(text, file_name,noise_multiplier,code_frequency,sample_rate, code_speed_wpm, zero_fill_to_N);
% morse(text, file_name,noise_multiplier,code_frequency,sample_rate, code_speed_wpm, zero_fill_to_N, play_sound);
%
% Description:
%
% If the wave file name is specified, then the funtion will output a wav
% file with that file name. If only text is specified, then the function
% will only play the morse code wav file without saving it to a wav file.
% If a noise multiplier is specified, zero mean addative white Gaussian
% noise is added with 'amplitude' noise_multiplier.
%
% Examples:
%
% morse('Hello');
% morse('How are you doing my friend?','morsecode.wav');
% morse('How are you doing my friend?','morsecode.wav', 0.01);
% morse('How are you doing my friend?','morsecode.wav', 0.01, 440, ,20, Fs);
% x = morse('How are you doing my friend?','morsecode.wav', 0.01, 440, 20, Fs, 2^20,1); %(to play the file, and make the length 2^20)
%
% Copyright 2005 Fahad Al Mahmood
% Version: 1.1 $ $Date: 08-Jul-2010
% Modifications: Rob Frohne, KL7NA
%Defualt values
Fs=48000;
noise_multiplier = 0;
f_code = 375;
code_speed = 20;
text = varargin{1}
if nargin>=2
file = varargin{2}
end
if nargin>=3
noise_multiplier = varargin{3};
end
if nargin>=4
f_code = varargin{4};
end
if nargin>=5
Fs = varargin{5};
end
if nargin>=6
code_speed = varargin{6};
end
if nargin>=7
length_N = varargin{7};
end
if nargin>=8
playsound = varargin{8};
end
t=0:1/Fs:1.2/code_speed; %One dit of time at w wpm is 1.2/w.
t=t';
Dit = sin(2*pi*f_code*t);
ssp = zeros(size(Dit));
#Dah fixed by Zach Swena
t2=0:1/Fs:3*1.2/code_speed; # one Dah of time is 3 times dit time
t2=t2';
Dah = sin(2*pi*f_code*t2);
lsp = zeros(size(Dah)); # changed size argument to function of Dah
#Dah = [Dit;Dit;Dit];
#lsp = zeros(size([Dit;Dit;Dit]));
% Defining Characters & Numbers
A = [Dit;ssp;Dah];
B = [Dah;ssp;Dit;ssp;Dit;ssp;Dit];
C = [Dah;ssp;Dit;ssp;Dah;ssp;Dit];
D = [Dah;ssp;Dit;ssp;Dit];
E = [Dit];
F = [Dit;ssp;Dit;ssp;Dah;ssp;Dit];
G = [Dah;ssp;Dah;ssp;Dit];
H = [Dit;ssp;Dit;ssp;Dit;ssp;Dit];
I = [Dit;ssp;Dit];
J = [Dit;ssp;Dah;ssp;Dah;ssp;Dah];
K = [Dah;ssp;Dit;ssp;Dah];
L = [Dit;ssp;Dah;ssp;Dit;ssp;Dit];
M = [Dah;ssp;Dah];
N = [Dah;ssp;Dit];
O = [Dah;ssp;Dah;ssp;Dah];
P = [Dit;ssp;Dah;ssp;Dah;ssp;Dit];
Q = [Dah;ssp;Dah;ssp;Dit;ssp;Dah];
R = [Dit;ssp;Dah;ssp;Dit];
S = [Dit;ssp;Dit;ssp;Dit];
T = [Dah];
U = [Dit;ssp;Dit;ssp;Dah];
V = [Dit;ssp;Dit;ssp;Dit;ssp;Dah];
W = [Dit;ssp;Dah;ssp;Dah];
X = [Dah;ssp;Dit;ssp;Dit;ssp;Dah];
Y = [Dah;ssp;Dit;ssp;Dah;ssp;Dah];
Z = [Dah;ssp;Dah;ssp;Dit;ssp;Dit];
period = [Dit;ssp;Dah;ssp;Dit;ssp;Dah;ssp;Dit;ssp;Dah];
comma = [Dah;ssp;Dah;ssp;Dit;ssp;Dit;ssp;Dah;ssp;Dah];
question = [Dit;ssp;Dit;ssp;Dah;ssp;Dah;ssp;Dit;ssp;Dit];
slash_ = [Dah;ssp;Dit;ssp;Dit;ssp;Dah;ssp;Dit];
n1 = [Dit;ssp;Dah;ssp;Dah;ssp;Dah;ssp;Dah];
n2 = [Dit;ssp;Dit;ssp;Dah;ssp;Dah;ssp;Dah];
n3 = [Dit;ssp;Dit;ssp;Dit;ssp;Dah;ssp;Dah];
n4 = [Dit;ssp;Dit;ssp;Dit;ssp;Dit;ssp;Dah];
n5 = [Dit;ssp;Dit;ssp;Dit;ssp;Dit;ssp;Dit];
n6 = [Dah;ssp;Dit;ssp;Dit;ssp;Dit;ssp;Dit];
n7 = [Dah;ssp;Dah;ssp;Dit;ssp;Dit;ssp;Dit];
n8 = [Dah;ssp;Dah;ssp;Dah;ssp;Dit;ssp;Dit];
n9 = [Dah;ssp;Dah;ssp;Dah;ssp;Dah;ssp;Dit];
n0 = [Dah;ssp;Dah;ssp;Dah;ssp;Dah;ssp;Dah];
text = upper(text);
vars ={'period','comma','question','slash_'};
morsecode=[];
for i=1:length(text)
if isvarname(text(i))
morsecode = [morsecode;eval(text(i))];
elseif ismember(text(i),'.,?/')
x = findstr(text(i),'.,?/');
morsecode = [morsecode;eval(vars{x})];
elseif ~isempty(str2num(text(i)))
morsecode = [morsecode;eval(['n' text(i)])];
elseif text(i)==' '
morsecode = [morsecode;ssp;ssp;ssp;ssp];
end
morsecode = [morsecode;lsp];
end
if exist('length_N','var')
append_length = length_N - length(morsecode);
if (append_length < 0)
printf("Length %d isn't large enough for your message; it must be > %d.\n",length_N,length(morsecode));
return;
else
morsecode = [morsecode; zeros(append_length,1)];
end
end
noisey_morsecode = morsecode + noise_multiplier*randn(size(morsecode));
SNR=20*log10(norm(morsecode)/norm(morsecode-noisey_morsecode));
printf('SNR =%f\n',SNR);
if exist('file','var')
wavwrite(noisey_morsecode,Fs,16,file);
if exist('playsound')
system(['aplay ',file]);
end
else
soundsc(noisey_morsecode,Fs);
% wavplay(morsecode);
end
code = noisey_morsecode;
endfunction







Interesting.
ReplyDeleteTim N9RO
hi Tim
DeleteDo you have any experience in extracting Morse code / CW signals using wavelets?
I stumbled on this topic just few weeks ago - see also this post.
Apparently wavelets are also commonly used in speech recognition and other applications where pulse timing provides important information.
Hello Mauri.
ReplyDeleteI am the person behind the PocketDigi, which is a port of the gmfsk application to the now dead PocketPC platform. PocketDigi was highly optimized to fixed point arithmetics running most of the HAM digital modes on a 200MHz ARM cpu.
I improved the original CW decoder of gmsk, which was reused by flDigi, by implementing a configurable boxcar filter after amplitude detection, which improved the detection considerably. I also implemented a Morse decoder using the same algorithm with a MSP430 no-multiplier controller doing all DSP filtering on a fixed audio frequency on the chip, drawing just 2mA at 3V.
I was pondering to apply AI methodology to Morse decoding. I studied neural networks and similar, but then my first son was born and my effort was mainly stopped by the need of collecting and manually segmenting Morse sound samples. As I am mostly interested into HF, I was thinking of generating the segmented sound samples with a ionospheric simulator:
http://www.johanforrer.net/SIMULR/index.html
http://wayback.archive.org/web/*/http://www.johanforrer.net/SIMULR/chansim-0.56-bns-3.tgz
http://www.moetronix.com/ae4jy/pathsim.htm
sm5bsz did an extensive research on impulse noise removal. His web is a bit untidy, but I believe it is worth to dive into it. I believe it is quite important to remove impulse noise before the signal is narrow band filtered as filtering of the noise spikes spreads them in time, the higher the peak the longer the spread.
http://www.sm5bsz.com/linuxdsp/usage/newco/newcomer.htm
While I was studying the neural network methods, I realized that a careful segmentation of the filtered signal will likely be more effectively processed by the neural network than just let's say a narrow band filtered amplitude envelope. I stumbled over the level set method for image segmentation. My gut felling is, it may work to extract the dots and dahs from the spectrogram even if the signal has not a stable frequency because of TX chirping or because of ionospheric effects.
http://math.berkeley.edu/~sethian/2006/Applications/Medical_Imaging/artery.html
And there is the CUDA architecture, which I bet would allow morse decoding on a wideband signal.
Thanks for resparking my interest into Morse code decoding once again and I am looking into finding a time to study your Morse decoding blog and the fldigi code thoroughly.
I would be happy to establish an e-mail contact. Would you please contact me at bubnikv at geeeemail (antispammed).
73, Vojtech OK1IAK, AB2ZA
Thanks for comments Vojtech. I sent you an email earlier today.
ReplyDelete73, Mauri AG1LE
Vojtech:
ReplyDelete> " As I am mostly interested into HF, I was thinking of generating the segmented sound samples with a ionospheric simulator"
What a great idea! I have been generating sound samples with Octave code from Rob, KL7NA. While it can generate Morse code with noise it is missing QSB, ionospheric multi-path timing etc. features present in real life signals. I look forward exchanging emails with you on this topic.
73 Mauri AG1LE